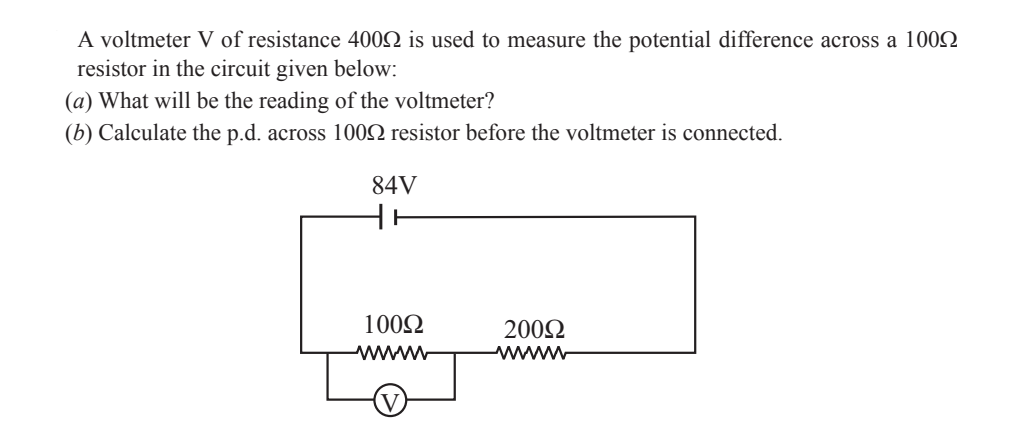
Combination of resistors – Saitech Informatics

To solve this problem, we need to determine the reading of a voltmeter with a resistance of 400Ω when connected across a 100Ω resistor, which is in series with a 200Ω resistor. Both resistors are connected to an 84V source. We’ll also calculate the potential difference across the 100Ω resistor before the voltmeter was connected.

### Part (a): Voltmeter Reading

When the voltmeter is connected across the 100Ω resistor, the voltmeter and the resistor form a parallel combination. This parallel branch is in series with the 200Ω resistor.

1. **Total Resistance of the Parallel Branch**:
– $R_{\text{parallel}} = \left(\frac{1}{100} + \frac{1}{400}\right)^{-1}$

2. **Total Resistance of the Circuit**:
– $R_{\text{total}} = R_{\text{parallel}} + 200$

3. **Total Current through the Circuit**:
– $I_{\text{total}} = \frac{V_{\text{source}}}{R_{\text{total}}}$

4. **Voltage across the Parallel Branch (Voltage read by the Voltmeter)**:
– $V_{\text{voltmeter}} = I_{\text{total}} \times R_{\text{parallel}}$

### Part (b): Voltage across the 100Ω Resistor Before Connecting the Voltmeter

Without the voltmeter, the resistors 100Ω and 200Ω are in series:
1. **Total Resistance without Voltmeter**:
– $R_{\text{total}}' = 100 + 200$

2. **Total Current through the Circuit without Voltmeter**:
– $I_{\text{total}}' = \frac{V_{\text{source}}}{R_{\text{total}}'}$

3. **Voltage across the 100Ω Resistor**:
– $V_{100} = I_{\text{total}}' \times 100$

Let’s perform the calculations now.

It seems there was an issue with the calculation. Let me try solving it again.

### Part (a): Voltmeter Reading

Given:
– Voltage source $V = 84V$
– Resistances: $R1 = 100\Omega$ , $R2 = 200\Omega$ , $R_{voltmeter} = 400\Omega$

For the parallel combination of the 100Ω resistor and the voltmeter:

$R_{parallel} = \left(\frac{1}{100} + \frac{1}{400}\right)^{-1}$

Total circuit resistance when the voltmeter is connected:

$R_{total} = R_{parallel} + 200$

Total current through the circuit:

$I_{total} = \frac{V_{source}}{R_{total}}$

Voltage across the parallel branch (and the voltmeter reading):

$V_{voltmeter} = I_{total} \times R_{parallel}$

### Part (b): Voltage across the 100Ω Resistor Before Connecting the Voltmeter

Total resistance of the 100Ω and 200Ω resistors in series:

$R_{total}' = 100 + 200$

Total current without the voltmeter:

$I_{total}' = \frac{V_{source}}{R_{total}'}$

Voltage across the 100Ω resistor before the voltmeter:

$V_{100} = I_{total}' \times 100$

Let’s perform these calculations manually, given the system issue:

#### For Part (a):
1. $R_{parallel} = \left(\frac{1}{100} + \frac{1}{400}\right)^{-1} = \left(0.01 + 0.0025\right)^{-1} = \left(0.0125\right)^{-1} = 80\Omega$
2. $R_{total} = 80\Omega + 200\Omega = 280\Omega$
3. $I_{total} = \frac{84V}{280\Omega} = 0.3A$
4. $V_{voltmeter} = 0.3A \times 80\Omega = 24V$

#### For Part (b):
1. $R_{total}' = 300\Omega$
2. $I_{total}' = \frac{84V}{300\Omega} = 0.28A$
3. $V_{100} = 0.28A \times 100\Omega = 28V$

Based on these manual calculations:
– The reading of the voltmeter (Part a) would be 24V.
– The voltage across the 100Ω resistor before connecting the voltmeter (Part b) would be 28V.

Translate

Related News

Semiconductors

Electrostatic Potential and Capacitance