Concepts
Geo means Earth
Metry means measurement
Statement – a sentence – either true or false – but cannot be both.
e.g. 3 + 8 = 10 false statement
3+ 8 = 11 = correct statement
Kala is fair. This is not a statement. because, for some persons she may look fair; for others she may not look fair.
Theorem – A statement that requires a proof.
Corollary – Result reduced from the theorem.
Point – it has no parts. e.g. a fine dot on the paper.
Line – no breadth, it has only length
It connects two points.
Surface – has length and breadth
Undefined terms – a point, a line, a plane
Axioms – postulates – assumptions or universal truth – not proved.
it is taken as it is.
1. If a = k, b = k, then a = b (things which are equal to the same are equal to one another)
2. If a = b, k is added on both sides,
a + k = b + k (if equals are added to equals, the wholes are equal.)
3. If a = b, k is subtracted from both sides,
a – k = b – k (if equals are subtracted from equals, the remainders are equal.)
4. Things which coincide with one another are equal to one another. If two things are identical, then they are equal.
5. The whole is greater than the part. a > a/k
6. If a = 2k, b = 2k, then a = b ( things which are double of the same thing are equal to one another)
7. If a = k/2, and b = k/2, then a = b (Things which are halves of the same thing are equal to one another)
- Euclid: Ancient Greek mathematician, known as the “Father of Geometry.”
- Axiomatic System: Euclid’s Geometry is based on a set of axioms (also known as postulates) and definitions as its foundation.
- Undefined Terms: Euclid’s system begins with three undefined terms: Point, Line, and Plane. These terms are not explicitly defined but serve as fundamental concepts.
- Postulates: Euclid’s system includes five postulates, which are basic assumptions about geometric objects and their relationships. For example, one postulate states that a straight line can be drawn between any two points.
- Common Notions: Euclid’s system also includes five common notions, which are general principles that apply to all of mathematics. These include principles like “Things that are equal to the same thing are equal to each other.”
- Theorems: Euclid’s Geometry consists of a series of theorems, which are proven statements based on the axioms, postulates, and common notions. These theorems form the body of geometric knowledge in Euclid’s work, “Elements.”
- Geometric Constructions: Euclid’s “Elements” also includes a section on geometric constructions. These are step-by-step procedures for using a compass and straightedge to create various geometric figures, such as bisecting an angle or constructing a perpendicular line.
- Parallel Postulate: Euclid’s fifth postulate, known as the Parallel Postulate, has been a subject of historical significance. It states that if a line crossing two other lines makes the interior angles on the same side less than two right angles, those two lines will eventually meet on that side. This postulate led to the development of non-Euclidean geometries.
- Legacy: Euclid’s work “Elements” is one of the most influential mathematical texts in history. It served as the foundation for the study of geometry for centuries and contributed to the development of axiomatic methods in mathematics. Even though some of Euclid’s postulates have been reevaluated, his system of geometry remains a critical part of mathematical history.
Euclid’s Five Postulates
1. A straight line can be drawn from any two points.
– This postulate allows the construction of lines by connecting two points.
2. A finite straight line can be extended indefinitely in a straight line.
– This postulate implies that a line can be extended infinitely in both directions.
3. A circle can be drawn with any centre and any radius.
– This postulate allows for the construction of circles of various sizes and positions.
4. All right angles are equal to each other.
– This postulate establishes the concept of right angles and their equality.
5. If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.
– This is known as the Parallel Postulate and deals with the behaviour of parallel lines. It’s the most debated of Euclid’s postulates and has led to the development of non-Euclidean geometries.
Problems based on Euclid’s Geometry
Problem 1: Construct an equilateral triangle given one of its sides.
Solution:
- Draw a line segment AB, which will be one side of the equilateral triangle.
- With A and B as centers and a radius equal to AB, draw two arcs that intersect at point C.
- Join AC and BC. Triangle ABC is the equilateral triangle you want.
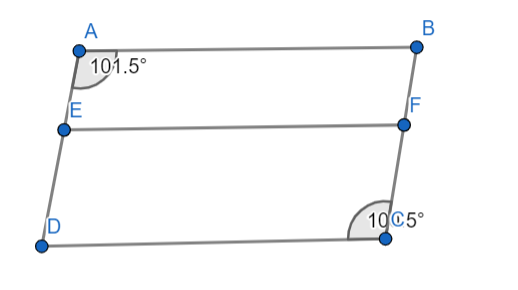
Problem 2: Prove that the opposite sides of a quadrilateral with a pair of opposite angles equal are parallel.
Solution:
Let ABCD be the given quadrilateral with ∠A = ∠C. To prove AB || CD:
- Draw a line through A parallel to CD. Let it intersect BC at E.
- Now, we have two pairs of alternate angles: ∠EAB ≅ ∠C and ∠A ≅ ∠C.
- Since corresponding angles are equal, AB || CD.
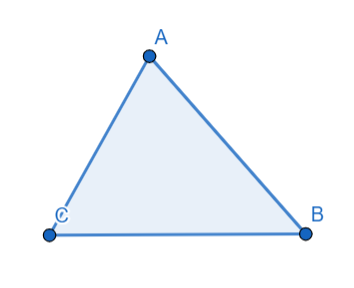
Problem 3: Prove that the sum of the angles of a triangle is 180 degrees.
Solution:
Consider triangle ABC.
- Draw a line segment DE parallel to BC passing through A.
- ∠ADE and ∠ACB are alternate angles and are equal by construction.
- ∠AED and ∠ABC are alternate angles and are equal by construction.
- ∠ADE + ∠AED + ∠ACB + ∠ABC = 180 degrees (because they form a straight line).
- ∠ADE + ∠AED + ∠ACB + ∠ACB = 180 degrees (because ∠ABC = ∠ACB).
- 2(∠ADE) + 2(∠ACB) = 180 degrees.
- ∠ADE + ∠ACB = 90 degrees (dividing both sides by 2).
- ∠A + ∠B + ∠C = 90 degrees + 90 degrees = 180 degrees.
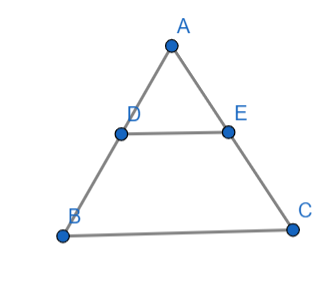
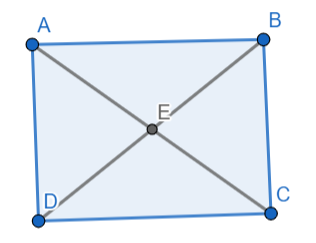
Problem 4: Prove that the diagonals of a rectangle are equal and bisect each other.
Solution:
Consider rectangle ABCD.
- AC is one diagonal.
- BD is the other diagonal.
- ∠ABC and ∠ADC are right angles (because they are angles of a rectangle).
- ∠ABC ≅ ∠ADC (both are right angles).
- AC is common to both triangles ABC and ADC.
- By ASA congruence, ΔABC ≅ ΔADC.
- Therefore, AB = AD and BC = DC.
- Hence, the diagonals AC and BD are equal and bisect each other.
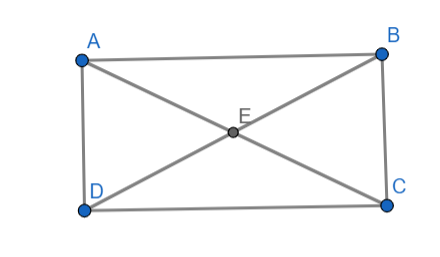
Problem 5: Prove that the opposite angles of a cyclic quadrilateral are supplementary.
Solution:
Consider a cyclic quadrilateral ABCD with vertices in that order on a circle.
- ∠ABC and ∠ADC are opposite angles.
- Both angles subtend the same arc CD.
- According to the theorem, angles subtended by the same arc at the center are equal.
- So, m∠ABC = m∠ADC.
- Therefore, ∠ABC and ∠ADC are supplementary because their angles add up to 180 degrees.
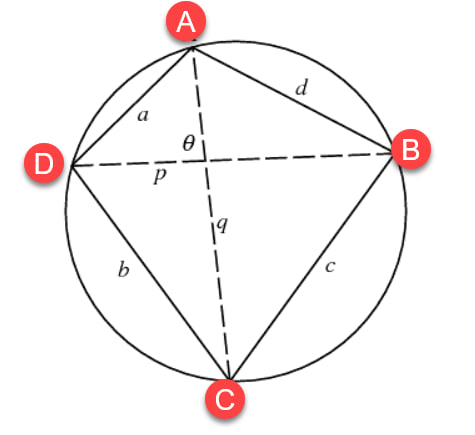
Problem 6: Prove that the sum of the angles of a quadrilateral is 360 degrees.
Solution:
Consider quadrilateral ABCD.
- Draw a diagonal AC, splitting the quadrilateral into two triangles, ABC and ADC.
- Using the result from Problem 3, the sum of angles in each triangle is 180 degrees.
- So, ∠A + ∠B + ∠C = 180 degrees and ∠A + ∠D + ∠C = 180 degrees.
- Adding these two equations together: ∠A + ∠B + ∠C + ∠A + ∠D + ∠C = 360 degrees.
- Simplifying, 2(∠A + ∠B + ∠C) + ∠D = 360 degrees.
- 2(180 degrees) + ∠D = 360 degrees.
- 360 degrees + ∠D = 360 degrees.
- ∠D = 0 degrees.
- Therefore, ∠A + ∠B + ∠C + ∠D = 360 degrees.
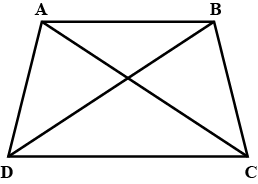
Problem 7: Prove that the opposite sides of a parallelogram are equal.
Solution:
Consider parallelogram ABCD.
- Draw diagonal AC, splitting the parallelogram into two congruent triangles, ABC and ADC.
- By the definition of a parallelogram, opposite sides are parallel. Therefore, AD || BC.
- Since ΔABC ≅ ΔADC by ASA congruence (common side AC, equal angles, and included side AB and AD), their corresponding sides are equal.
- So, AB = AD.
- Therefore, the opposite sides of the parallelogram ABCD are equal.
Problem 8: Prove that the diagonals of a square are perpendicular to each other and bisect each other.
Solution:
Consider square ABCD.
- Draw diagonal AC, splitting the square into two congruent triangles, ABC and ADC.
- Since all angles of a square are right angles (90 degrees), both ∠ABC and ∠ADC are 90 degrees.
- By definition, opposite sides of a square are equal.
- So, AB = BC = CD = DA.
- In ΔABC, AB = BC, and ∠ABC = ∠BCA = 90 degrees.
- This implies that ΔABC is an isosceles right triangle.
- In an isosceles right triangle, the hypotenuse (AC) is the longest side, and the other two sides (AB and BC) are equal.
- So, AB = BC < AC (by the Pythagorean theorem).
- Similarly, in ΔADC, AD = DC < AC.
- Therefore, the diagonals of the square ABCD are perpendicular to each other and bisect each other.
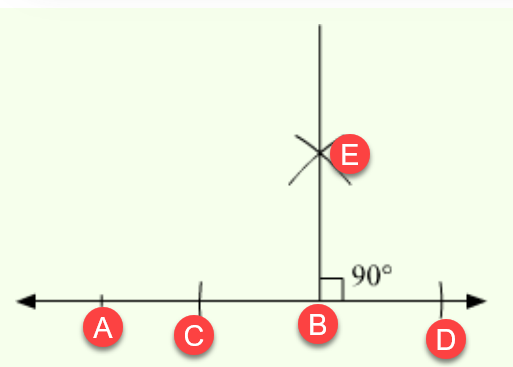
Problem 9: Given a line segment AB, construct a line perpendicular to AB at point B.
Solution:
- Draw a line segment AB.
- With point B as the center and any radius, draw an arc that intersects AB at two points, say C and D.
- Draw arcs with the same radius and centers at C and D to intersect each other at point E.
- Line BE is the perpendicular line to AB at point B.
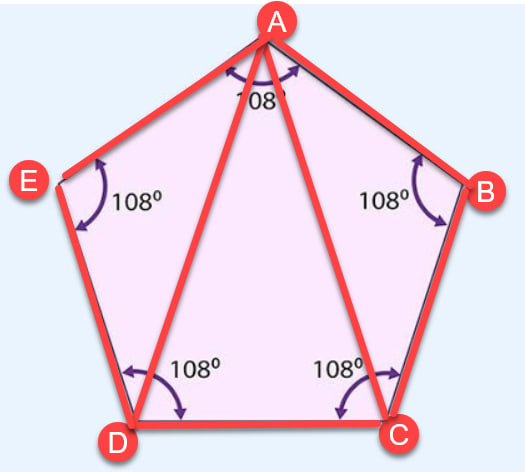
Problem 10: Prove that the sum of the angles of a pentagon is 540 degrees.
Solution:
Consider pentagon ABCDE.
- Draw diagonal AC, splitting the pentagon into three triangles: ABC, ACD, and ADE.
- Using the result from Problem 6, each triangle’s angles sum to 180 degrees.
- So, ∠A + ∠B + ∠C = 180 degrees, ∠A + ∠C + ∠D = 180 degrees, and ∠A + ∠D + ∠E = 180 degrees.
- Add these three equations together: ∠A + ∠B