Here are Euclid’s five common notions (axioms):
- Things which are equal to the same thing are also equal to one another. (This is essentially a statement of the transitive property of equality.)
- If equals are added to equals, the wholes are equal. (If you add the same amount to two equal quantities, the resulting sums will still be equal.)
- If equals are subtracted from equals, the remainders are equal. (Similarly, if you subtract the same amount from two equal quantities, the resulting differences will still be equal.)
- Things which coincide with one another are equal to one another. (This is a basic statement about the nature of equality in geometry. If two geometric figures can be perfectly superimposed on each other, they are equal in every respect.)
- The whole is greater than the part. (Any portion of a geometric entity will be less than the entirety of that entity.)
Euclid’s Postulates: To give a concrete example, here are the five postulates from Euclid’s “Elements” that form the foundation of Euclidean geometry:
- A straight line segment can be drawn joining any two points.
- Any straight line segment can be extended indefinitely in a straight line.
- Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
- All right angles are congruent.
- If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines will meet on that side if extended far enough. This is the famous “parallel postulate.”
Problem
Prove that an equilateral triangle can be constucted on any given line segment.
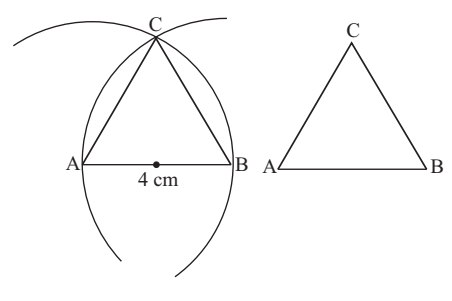
- A circle is drawn taking the point A as centre and AB as radius.
- An another circle or arc is drawn taking the point B as centre and AB as radius.
- The two arcs meet at C.
- A triangle, ABC is drawn.
- According to Euclid’s axiom, AB = AC = BC, AB = BC. Hence triangle ABC is an equilateral triangle.


